1. 问题

之前遇到过这么一个问题{:target="_blank"} ，说有一只青蛙，它想跳到 n 层的楼梯上面去，由于自身原因，它每次只能选择跳 1 层或者 2 层。
问，青蛙有多少种跳法？

第一眼看到这个问题的时候有点蒙，不知道从何下手。不妨先从可见的楼梯层数 n 入手，设求青蛙跳法的方法是 f(n)。
那么当 n=1 时 f(n)=1, n=2 时 f(n)=2, n=3 时 f(n)=3, n=4 时 f(n)=5 …
很明显，f(n) 是一个斐波那锲数列的方法，当前数等于前两个数之和，所以有 f(n)=f(n-1)+f(n-2)。
其实从另一个角度想也可以想明白，假设我是那只青蛙，站在 n 层的楼梯脚下，我有 f(n) 种跳法，现在我能选择的是跳 1 层还是跳 2 层。当我选择跳 1 层时，我接下来的跳法还有 f(n-1) 种；当我选择跳 2 层时，我接下来的跳法还有 f(n-2) 种。所以我在还没有选择之前的跳法应该等于我这两种跳法之和，所以有 f(n)=f(n-1)+f(n-2)。

2. 解答

2.1 递归

上面的思路有了，我们很容易就可以用代码实现了。

public int climbStairs(int n) {
    if (n <= 0) return 0;
    if (n == 1) return 1;
    if (n == 2) return 2; 
    // f(n)=f(n-1)+f(n-2)
    return climbStairs(n - 1) + climbStairs(n - 2);
}

上面的代码虽然可以解决问题，但是会出现很大一部分的重复运算。如下图所示，当 n=6 时，我们计算了 2 次 f(4), 3 次 f(3)。 f(6)

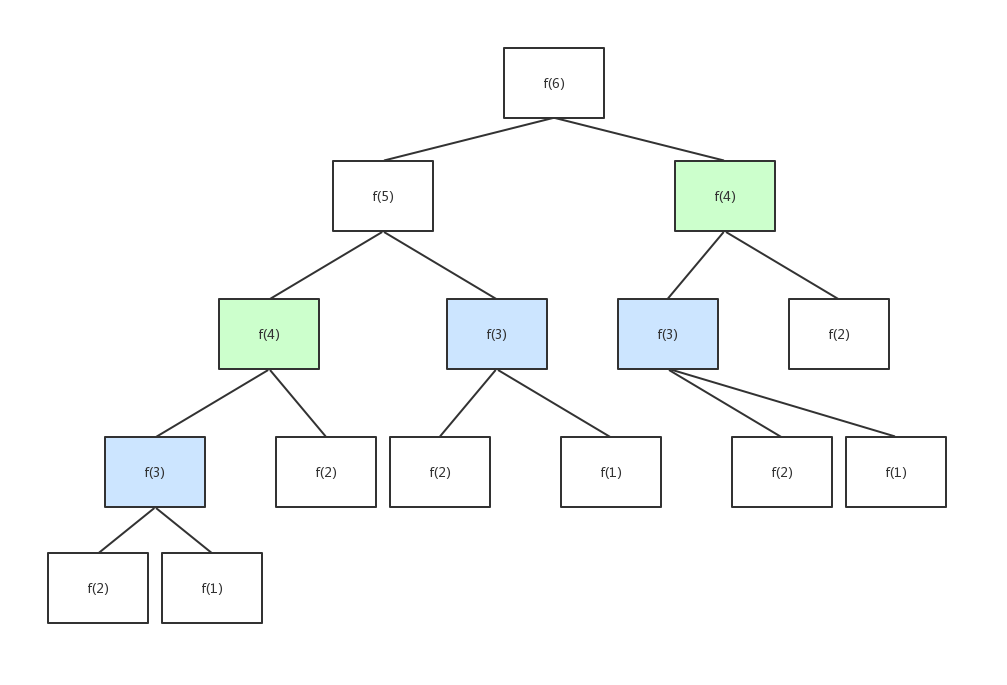
2.2 备忘录模式

基于上面的问题，我们可以使用备忘录模式，维护一个 map ，key 表示台阶层数 n，value 表示跳法。把计算过的结果放在 map 中，在开始计算之前先检查下备忘录 map 中是否已经有对应的结果了，如果没有再计算，并把计算完成后的结果添加到备忘录 map 中。

Map<Integer, Integer> memoMap = new HashMap<>();

public int climbStairs(int n) {
    // 检查备忘录中是否已经存在相应结果
    if (memoMap.containsKey(n)) {
        return memoMap.get(n);
    }
    int result;
    if (n <= 0) {
        result = 0;
    } else if (n == 1) {
        result = 1;
    } else if (n == 2) {
        result = 2;
    } else {
        result = climbStairs(n - 1) + climbStairs(n - 2);
    }
    // 计算完成之后把结果添加到备忘录中
    memoMap.put(n, result);
    return result;
}

2.3 迭代

我们知道，递归可以优化成迭代，我们该如何做呢？
递归可以理解为是自上而下的解决问题，不断的把问题分解成一个个的小问题，直到得到这一个个的小问题答案后，再汇集成整个问题的答案。
迭代可以理解为是自下而上的解决问题，不断的累计一个个的小问题的答案，直到累计得到大问题的答案。

public int climbStairs(int n) {
    if (n <= 0) return 0;
    if (n == 1) return 1;
    if (n == 2) return 2;
    // 定义数组记录下标为 n 对应的跳法
    int[] resultArray = new int[n];
    resultArray[0] = 1;
    resultArray[1] = 2;
    for (int i = 2; i < n; i++) {
        resultArray[i] = resultArray[i - 1] + resultArray[i - 2];
    }
    return resultArray[n - 1];
}

3. 总结

3.1 动态规划的定义

什么是动态规划，我在维基百科{:target="_blank"} 查到的定义如下。
动态规划（英语：Dynamic programming，简称 DP）是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的，通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。

3.2 适用情况

最优子结构性质。如果问题的最优解所包含的子问题的解也是最优的，我们就称该问题具有最优子结构性质（即满足最优化原理）。最优子结构性质为动态规划算法解决问题提供了重要线索。
无后效性。即子问题的解一旦确定，就不再改变，不受在这之后、包含它的更大的问题的求解决策影响。
子问题重叠性质。子问题重叠性质是指在用递归算法自顶向下对问题进行求解时，每次产生的子问题并不总是新问题，有些子问题会被重复计算多次。动态规划算法正是利用了这种子问题的重叠性质，对每一个子问题只计算一次，然后将其计算结果保存在一个表格中，当再次需要计算已经计算过的子问题时，只是在表格中简单地查看一下结果，从而获得较高的效率。

3.2 解法步骤

描述最优解的结构特征
递归地定义一个最优解的值
自底向上计算一个最优解的值
从已计算的信息中构造一个最优解

1. 问题#

2. 解答#

2.1 递归#

2.2 备忘录模式#

2.3 迭代#

3. 总结#

3.1 动态规划的定义#

3.2 适用情况#

3.2 解法步骤#