最短路径-迪杰斯特拉

/**
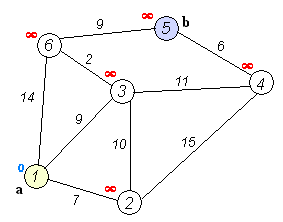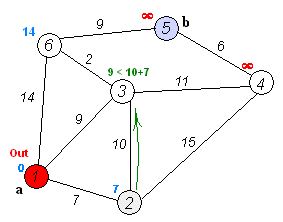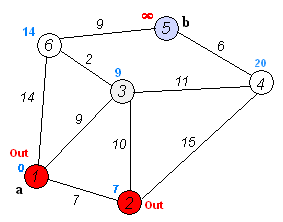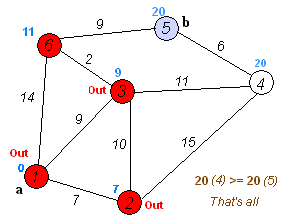
 * 迪杰斯特拉算法求最短路径
 * @author sunbufu
 *
 */
public class ShortestPathDijkstra {
	/**无穷大*/
	final static int INF = Integer.MAX_VALUE;

	public static void main(String[] args) {
		int[] points = { 1, 2, 3, 4, 5, 6 };
		int[][] weights = {
//				 1    2    3    4    5    6
				{0,   7,   9,   INF, INF, 14   },//1
				{7,   0,   10,  15,  INF, INF  },//2
				{9,   10,  0,   11,  INF, 2    },//3
				{INF, 15,  11,  0,   6,   INF  },//4
				{INF, INF, INF, 6,   0,   9    },//5
				{14,  INF, 2,   INF, 9,   0    } //6
		};
		dijkstra(points, weights);
	}

	public static void dijkstra(int[] points, int[][] weights) {
		int pointsNumber = points.length;
		boolean[] finsih = new boolean[pointsNumber];// 是否已经确定该点的最短路径
		int[] shortestPathWeights = new int[pointsNumber];// 最短路径的权值
		int[] previousPoint = new int[pointsNumber];// 路径中，该结点的上一个结点
		// 初始化
		for (int i = 1; i < pointsNumber; i++) {
			shortestPathWeights[i] = weights[0][i];
			finsih[i] = false;
			if (shortestPathWeights[i] == INF)// 如果跟起点没有直接关联
				previousPoint[i] = -1;// 上一结点置为无效
			else
				previousPoint[i] = 0;// 否则上一结点置为起点
		}
		finsih[0] = true;
		// 计算距离起点的最短路径
		for (int i = 1; i < pointsNumber; i++) {
			int shortestPath = INF;
			int point = 0;// 当前未被最终确定的节点中，离起点最近的
			for (int j = 0; j < pointsNumber; j++) {// 寻找距离起点最近的顶点
				if (!finsih[j] && shortestPathWeights[j] < shortestPath) {// 没有被最终确定，并且该距离小于上一个
					shortestPath = shortestPathWeights[j];
					point = j;
				}
			}
			finsih[point] = true;
			// 计算跟其余已知最短路径的，修正最短路径
			for (int j = 0; j < pointsNumber; j++) {
				if (!finsih[j] && weights[point][j] < INF) {
					if (shortestPathWeights[point] + weights[point][j] < shortestPathWeights[j]) {// 如果通过point，更新距离起点更短的路径
						shortestPathWeights[j] = shortestPathWeights[point] + weights[point][j];
						previousPoint[j] = point;
					}
				}
			}
		}
		for (int i = 0; i < pointsNumber; i++) {
			System.out.println(points[i] + "\t最短路径的权值 = " + shortestPathWeights[i] + ",\t上一个结点 = " + previousPoint[i]);
		}
	}

}